➤ 算法 | ⭐️二分查找

(Updated: )

二分查找

1. 区间设定

推荐左闭右开：[left, right)。

1
2
3
4
int left = 0, right = arr.length;
while (left < right) {
    // TODO
}

问：这里为什么不能是 while (left <= right) ？
答：因为左闭右开区间，反例：[1, 1)，既包含 1，又不包含 1，矛盾。

2. mid 值计算

推荐：left + (right - left) / 2 或 int mid = left + ((right - left) >> 1)，可以防止 left + right 越界。

1
2
3
4
5
6
7
8
9
public class HelloWorld {
	public static void main(String []args) {
		int left = Integer.MAX_VALUE;
		int right = 2;
		System.out.println((left + right) / 2); // 打印：-1073741823
		System.out.println((left + right) >> 1); // 打印：-1073741823
		System.out.println(left + (right - left) / 2); // 打印：1073741825
	}
}

3. if 与 return

一般来说分三种情况：

  • tar < arr[mid]：左移右指针，right = mid；

  • arr[mid] < tar：右移左指针，left = mid + 1；

  • arr[mid] == tar：根据不同情况，做不同处理：

    • == tar：return mid，如果没有找到 tar，则最后返回 -1；
    • ≥ tar 的最小值：左移右指针，right = mid，return left；
    • < tar 的最大值：左移右指针，right = mid，return left - 1；
    • ≤ tar 的最大值：右移左指针，left = mid + 1，return left - 1；
    • > tar 的最小值：右移左指针，left = mid + 1，return left。

4. 特别注意

  • 在返回对应值时，注意 left 或 left - 1 是在 [0, arr.length) 区间的；
  • 有时 arr 里不存在 tar 值，需要根据题意特殊判断一下，比如 if(arr[left] != tar) {...}。

模板总结

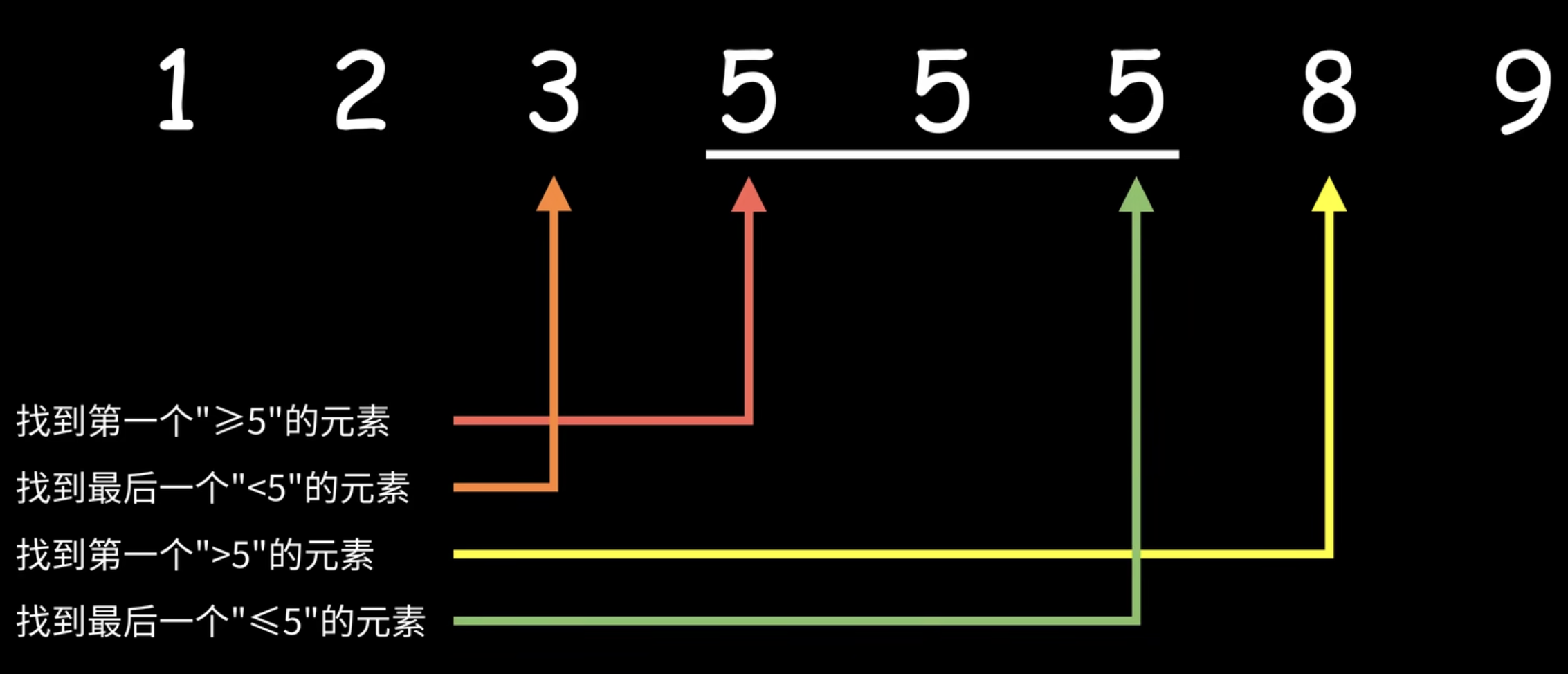
image-20230903161010786

等值情况下，很好判断，比较难记的是边界，这里给出总结，便于记忆：

arr[mid] == tar 时的指针移动：

  • 目标是图中左侧橙色、红色的值，则 right = mid；
  • 目标是图中右侧绿色、黄色的值，则 left = mid + 1。

return 值：

  • 目标是图中红色、黄色的值，则 return left；
  • 目标是图中橙色、绿色的值，则 return left - 1。
right = mid left = mid + 1
return left 红 黄
return left - 1 橙 绿

特别地，在寻找 ≥ tar 的最小值的位置时，如果 tar 不存在于数组中，那么返回的是 tar 要插入的位置，这个位置可能是 -1，也可能是 arr.length。

1. == tar

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public class Main {
    public static void main(String []args) {
		int[] arr = new int[]{1,2,3,5,5,5,8,9};
		int tar = 5;
	    System.out.println(binarySearch(arr, tar)); // 4
    }
	public static int binarySearch(int[] arr, int tar) {
		int left = 0, right = arr.length;
		while (left < right) {
			int mid = left + (right - left) / 2;
			if (arr[mid] == tar) {
				return mid; // ❗️mid 即为所求
			} else if (arr[mid] < tar) {
				left = mid + 1;
			} else if (tar < arr[mid]) {
				right = mid;
			}
		}
		return -1; // ❗️不存在 tar，返回 -1
	}
}

2. ≥ tar 的最小值的位置

翻译：tar 第一次出现的位置；tar 左边界；……

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
public class Main {
    public static void main(String []args) {
		int[] arr = new int[]{1,2,3,5,5,5,8,9};
		int tar = 5;
	    System.out.println(binarySearch(arr, tar)); // 2
    }
	public static int binarySearch(int[] arr, int tar) {
		int left = 0, right = arr.length;
		while (left < right) {
			int mid = left + (right - left) / 2;
			if (arr[mid] == tar) {
				right = mid; // ❗️
			} else if (arr[mid] < tar) {
				left = mid + 1;
			} else if (tar < arr[mid]) {
				right = mid;
			}
		}
        // 里不存在 tar
        if (left < 0 || left >= arr.length) return -1; 
        if (tar != arr[left]) return -1;
		return left; // ❗️
	}
}

3. ≤ tar 的最大值的位置

翻译：tar 最后一次出现的位置；tar 右边界；……

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
public class Main {
    public static void main(String []args) {
		int[] arr = new int[]{1,2,3,5,5,5,8,9};
		int tar = 5;
	    System.out.println(binarySearch(arr, tar)); // 5
    }
	public static int binarySearch(int[] arr, int tar) {
		int left = 0, right = arr.length;
		while (left < right) {
			int mid = left + (right - left) / 2;
			if (arr[mid] == tar) {
				left = mid + 1; // ❗️
			} else if (arr[mid] < tar) {
				left = mid + 1;
			} else if (tar < arr[mid]) {
				right = mid;
			}
		}
        // 里不存在 tar
        if (left - 1 < 0 || left - 1 >= arr.length) return -1; 
        if (tar != arr[left - 1]) return -1;
		return left - 1; // ❗️
	}
}

4. > tar 的最小值的位置

翻译：tar 最后一次出现的位置的下一个位置；> tar 的第一个位置；……

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public class Main {
    public static void main(String []args) {
		int[] arr = new int[]{1,2,3,5,5,5,8,9};
		int tar = 5;
	    System.out.println(binarySearch(arr, tar)); // 6
    }
	public static int binarySearch(int[] arr, int tar) {
		int left = 0, right = arr.length;
		while (left < right) {
			int mid = left + (right - left) / 2;
			if (arr[mid] == tar) {
				left = mid + 1; // ❗️
			} else if (arr[mid] < tar) {
				left = mid + 1;
			} else if (tar < arr[mid]) {
				right = mid;
			}
		}
		return left; // ❗️
	}
}

5. < tar 的最大值的位置

翻译：tar 第一次出现的位置的前一个位置；< tar 的最后一个位置；……

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public class Main {
    public static void main(String []args) {
		int[] arr = new int[]{1,2,3,5,5,5,8,9};
		int tar = 5;
	    System.out.println(binarySearch(arr, tar)); // 2
    }
	public static int binarySearch(int[] arr, int tar) {
		int left = 0, right = arr.length;
		while (left < right) {
			int mid = left + (right - left) / 2;
			if (arr[mid] == tar) {
				right = mid; // ❗️
			} else if (arr[mid] < tar) {
				left = mid + 1;
			} else if (tar < arr[mid]) {
				right = mid;
			}
		}
		return left - 1; // ❗️
	}
}

力扣练习